TiferKing的学习笔记
这里记录了TiferKing的学习历程
-
TPS5430 负压工作时 使能(EN)信号的正压控制转换
最近在做项目的时候遇到了一个问题，一开始的时候完全没有想到会遇到这种问题，只能说经验还是有点匮乏。就是在使用T…
-
Dell C6320p 调试记录 (附电源板PCB)
之前大概12年到13年的时候，听说Intel出了一款非常厉害的协处理器叫Xeon Phi，有六十多个核心外加每…
-
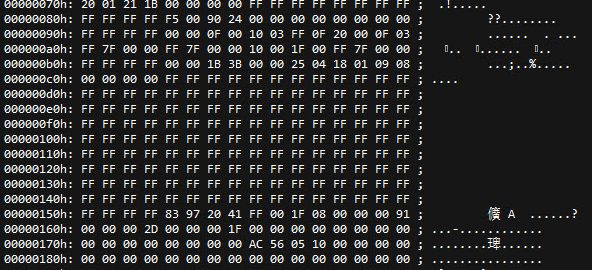
Dell 13代服务器 修改 Service Tag
感觉有很长一段时间没有写博客了，有时候想起来还有点愧疚，毕竟最开始的时候励志要把自己学到的新东西记下来。（或者…
-
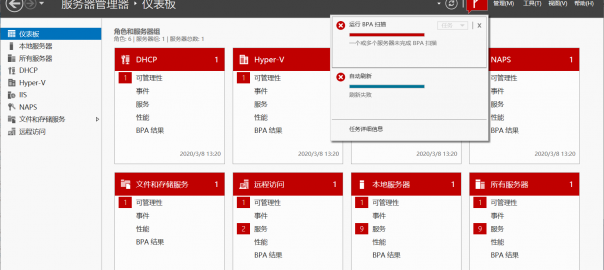
Windows Server 无法获得 BPA 结果
最近维护服务器的时候碰见了这个错误，看到网上很少有人讨论，所以大概记录一下。 系统版本：Windows Ser…
-
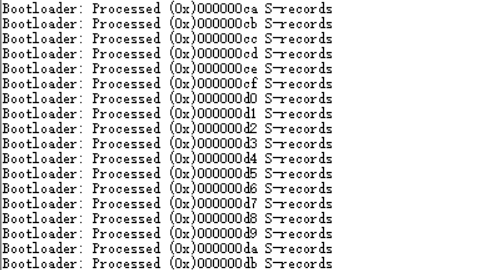
MicroBlaze 不使用 片上 RAM 实现上电自启
最近在学Xilinx公司的开发流程，正巧学到了MicroBlaze处理器，由于使用的这款VC707开发板没有像…
-
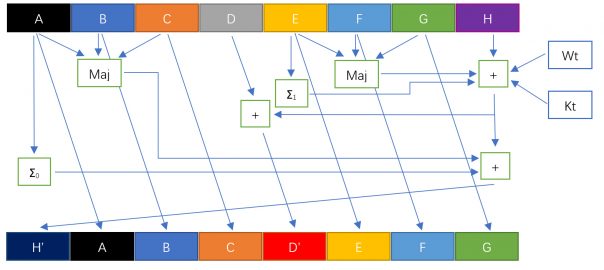
SHA-256 摘要算法 实现 及 优化
很久没有发文章了啊，咳咳，最近考试考的人心力交瘁。这两天由于需要(真的是自已的需要么？)，做了做摘要算法方面的…
-
戴尔 R730 风扇转速过高 噪声过大 调整记录
昨天安装新服务器的时候发现了一个问题，那就是当服务器进入操作系统之后风扇转速便超过了80%，在BIOS里边设置…
-
AMD Radeon Vega Frontier Edition 与 Windows Server 2016 的调整小记
最近入手了一块农企的显卡，Vega Frontier Edition。本来是一件令人兴奋的事情，但是在使用的过…
-
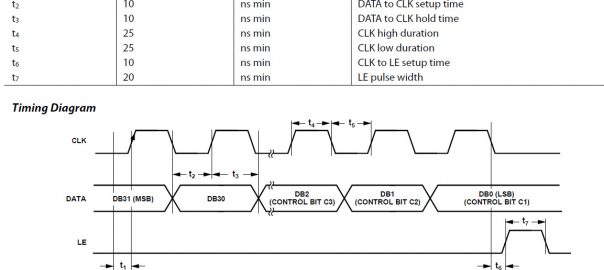
ADF4251 锁相环 使用笔记 (配合HAL库)
之前在比赛准备的时候有准备过关于锁相环相关的器件，这里介绍一下ADF4351这款宽带频率合成器的使用。 由于我…
-
瑞萨杯 电赛 2017年H题 远程幅频特性测试装置 题简解
已经有半年多没有更新过博客了啊，这段时间一直是忙的不可开交，总觉得浪费点时间来写博客是一件特别奢侈的事情。不过…
-
记录一次boot sector的编写
前段时间学了一点点关于操作系统的东西，跟着一本分析Linux 0.11 内核代码的书学习的，刚开始的时候，书中…
-
第三章：C++中的C
在使用C++编写程序的时候，我们会发现其中很多地方所使用的语句与C语言十分相似，其实从其命名可以看出来，C++…