很久没有发文章了啊,咳咳,最近考试考的人心力交瘁。这两天由于需要(真的是自已的需要么?),做了做摘要算法方面的工作,以前都是调库,但是现在需要将算法移植到stm32上,不仅要保证功能性还要保证效率,于是自己编写了一个SHA-256的程序,现分享一下。
作为哈希算法在我印象中最早听说的是md5算法,不过后来又听说它被发现有一些弱点,其发现者是我国的密码学专家王小云教授,不过虽然其弱点被发现,也并不影响其在一些领域的应用,至今我还经常能看到md5的身影。当然我这里选用了相对安全一些的SHA-256算法,SHA全称为Secure Hash Algorithm,意为安全哈希算法,其算法到目前为止历经了三代的变革,SHA-1,SHA-2和SHA-3,而SHA-256是SHA-2系列中的一个算法,那么先从SHA-256算法本身开始讲起。
哈希做为一个摘要算法,直观上讲,不管给其输入什么内容,其结果最终都会是一个固定长度的码串。对于SHA-256,其输出的长度便是256bit,也就是说所有的数据都可以映射到这个2^256个值的域中。也就是说其与普通上讲的加密算法有所不同的是,哈希算法会将输入的信息损失一部分,因为其值域是有限的,而定义域却是无限的。所以经过这种算法处理,其结果是不能逆向求得值的。(其实哈希算法并不能算作加密算法)
比方在网站存储用户密码的时候,为了防止入侵者入侵数据库后直接拿到用户的密码,往往会使用哈希函数对用户的密码进行处理,这样每当用户登录的时候便可以将用户提交的密码进行同样的运算来对比结果验证身份,同样可以保证在数据库被入侵后用户的密码一定程度上不会完全泄露(简单的密码也就查个表的事,和裸奔没区别)。当然这只是其中一个小应用,其在数字签名,文件防伪等方面也有广泛应用,甚至说是比特币这样的区块链货币的核心算法也不为过。
SHA-256算法的过程
首先我想简单直白的总结一下SHA-256的算法过程。
第一步:先对输入的数据进行补位和分块,SHA-256算法的数据分为512bit一个区块。然后循环的做迭代运算,直到算出结果。由于数据并非一定是512bit的整数倍,所以需要先进行补位,使其成为512bit块的整数倍。补位的操作为向数据后先补1位1然后补0至位长度对512取模为448为止,然后再在末尾添加一个64位长的数据长度字。
这里需要详细说一下,因为一开始我也有点犯晕,比方说你现在有一个信息为“01010”,那么你的补位结果是“0101010000…(省略496个“0”)…000101”,最后一位这个长度字的数值为你输入的数据的bit数。当然在计算机当中一般也不会碰到非整byte的信息,所以这个长度往往是8的倍数,而在进行补1操作时,往往也是在后面跟一个0x80字节。当然一旦你输入的信息超过了448bit那么就必须向数据后添加新的一个512bit区块来补位,这个新的区块可能仅包含0x00和长度字。
我将其总结为以下三种情况:
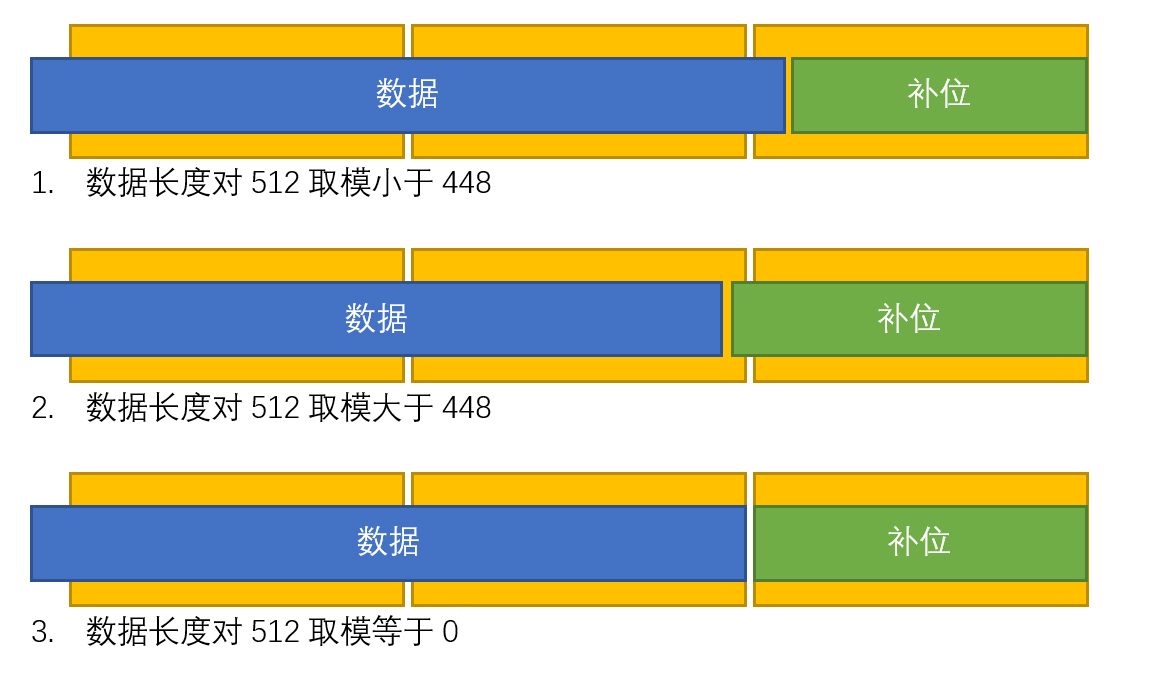
这样对其分类我们可以采取三种简便的方法来补位。
第二步:对区块进行混合。这里便需要介绍SHA-256的几种混合函数:
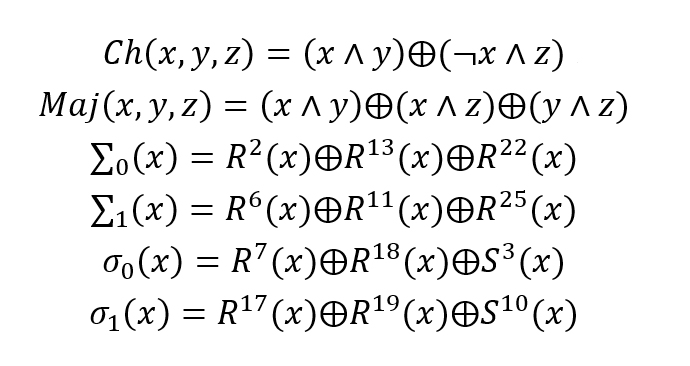
其中符号含义为:

SHA-256便是利用这几种混合函数对数据进行混合,值得注意的是,这里前两种函数Ch(x)和Maj(x)对数据进行处理时便已经产生了信息的损失,而后四种函数则是一一对应的,没有损失任何信息。(这里并不是凭空臆测其输入bit与输出bit便草草得出结论,而是经过了程序枚举验证,四个函数的定义域与值域均是一一映射的。)(内存大就是为所欲为)
其混合过程可以由下图总结(图中仅为一轮混合):

图中每一个色块表示32bit的数据,绿色框线中的“+”表示32位加法,剩下的便是混合公式,蓝色框线中为混合时输入的数据。Wt是由用户输入的数据经过变换得来的,而Kt为已知常数。将图中的混合过程迭代重复64次,便可得到最终的SHA-256值。
其中最初的A-H值为:
A = 0x6a09e667; B = 0xbb67ae85; C = 0x3c6ef372; D = 0xa54ff53a; E = 0x510e527f; F = 0x9b05688c; G = 0x1f83d9ab; H = 0x5be0cd19;
这8个值分别为前8个质数(2,3,5,7,11,13,17,19)的平方根取小数部分前32bit。混合时使用的常数Kt为:
uint32_t K[] = {
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2};
这64个值则是前64个质数的立方根取小数部分前32bit而来。(事实上我觉得这些取值没什么理论依据,就跟我一拍大腿想出来的一样,看起来很混乱就是了)
Wt是用户需要做SHA-256变换输入的数据,其中前16轮变换输入的数据为一个512bit区块分割为16个32bit区块顺序填入的值。而第17至64轮变换时,Wt的生成公式为:
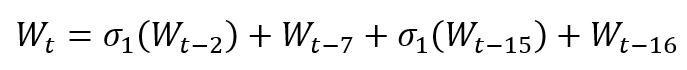
当64轮混合做完了之后,将变换结果以每32位为一块与变换前的值做加法,便得到了最终的SHA-256摘要值。如果区块不止一块的话则将前一块的摘要值作为下一块的初始值,继续进行64轮变换,直到迭代到最后一块区块变换完成为止。
第三步:将最终的结果返回便是该输入信息的SHA-256哈希值。
SHA-256算法实现
搜索GitHub便可得到很多SHA-256的实现代码,比如Openssl中就包含SHA-256的实现,还有Crypto++,BitCoin等,其中的代码均可借鉴。
其中Openssl的SHA-256算法实现可以说非常的清晰易懂:
static void sha256_block_data_order(SHA256_CTX *ctx, const void *in,
size_t num)
{
unsigned MD32_REG_T a, b, c, d, e, f, g, h, s0, s1, T1, T2;
SHA_LONG X[16], l;
int i;
const unsigned char *data = in;
while (num--) {
a = ctx->h[0];
b = ctx->h[1];
c = ctx->h[2];
d = ctx->h[3];
e = ctx->h[4];
f = ctx->h[5];
g = ctx->h[6];
h = ctx->h[7];
for (i = 0; i < 16; i++) {
(void)HOST_c2l(data, l);
T1 = X[i] = l;
T1 += h + Sigma1(e) + Ch(e, f, g) + K256[i];
T2 = Sigma0(a) + Maj(a, b, c);
h = g;
g = f;
f = e;
e = d + T1;
d = c;
c = b;
b = a;
a = T1 + T2;
}
for (; i < 64; i++) {
s0 = X[(i + 1) & 0x0f];
s0 = sigma0(s0);
s1 = X[(i + 14) & 0x0f];
s1 = sigma1(s1);
T1 = X[i & 0xf] += s0 + s1 + X[(i + 9) & 0xf];
T1 += h + Sigma1(e) + Ch(e, f, g) + K256[i];
T2 = Sigma0(a) + Maj(a, b, c);
h = g;
g = f;
f = e;
e = d + T1;
d = c;
c = b;
b = a;
a = T1 + T2;
}
ctx->h[0] += a;
ctx->h[1] += b;
ctx->h[2] += c;
ctx->h[3] += d;
ctx->h[4] += e;
ctx->h[5] += f;
ctx->h[6] += g;
ctx->h[7] += h;
}
}
Openssl这里代码写的非常规整,当然这只是作为原理示范代码,其真正使用的代码是用汇编语言编写的。再列举一个BitCoin的代码:
void Transform(uint32_t* s, const unsigned char* chunk, size_t blocks)
{
while (blocks--) {
uint32_t a = s[0], b = s[1], c = s[2], d = s[3], e = s[4], f = s[5], g = s[6], h = s[7];
uint32_t w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14, w15;
Round(a, b, c, d, e, f, g, h, 0x428a2f98 + (w0 = ReadBE32(chunk + 0)));
Round(h, a, b, c, d, e, f, g, 0x71374491 + (w1 = ReadBE32(chunk + 4)));
Round(g, h, a, b, c, d, e, f, 0xb5c0fbcf + (w2 = ReadBE32(chunk + 8)));
Round(f, g, h, a, b, c, d, e, 0xe9b5dba5 + (w3 = ReadBE32(chunk + 12)));
Round(e, f, g, h, a, b, c, d, 0x3956c25b + (w4 = ReadBE32(chunk + 16)));
Round(d, e, f, g, h, a, b, c, 0x59f111f1 + (w5 = ReadBE32(chunk + 20)));
Round(c, d, e, f, g, h, a, b, 0x923f82a4 + (w6 = ReadBE32(chunk + 24)));
Round(b, c, d, e, f, g, h, a, 0xab1c5ed5 + (w7 = ReadBE32(chunk + 28)));
Round(a, b, c, d, e, f, g, h, 0xd807aa98 + (w8 = ReadBE32(chunk + 32)));
Round(h, a, b, c, d, e, f, g, 0x12835b01 + (w9 = ReadBE32(chunk + 36)));
Round(g, h, a, b, c, d, e, f, 0x243185be + (w10 = ReadBE32(chunk + 40)));
Round(f, g, h, a, b, c, d, e, 0x550c7dc3 + (w11 = ReadBE32(chunk + 44)));
Round(e, f, g, h, a, b, c, d, 0x72be5d74 + (w12 = ReadBE32(chunk + 48)));
Round(d, e, f, g, h, a, b, c, 0x80deb1fe + (w13 = ReadBE32(chunk + 52)));
Round(c, d, e, f, g, h, a, b, 0x9bdc06a7 + (w14 = ReadBE32(chunk + 56)));
Round(b, c, d, e, f, g, h, a, 0xc19bf174 + (w15 = ReadBE32(chunk + 60)));
Round(a, b, c, d, e, f, g, h, 0xe49b69c1 + (w0 += sigma1(w14) + w9 + sigma0(w1)));
Round(h, a, b, c, d, e, f, g, 0xefbe4786 + (w1 += sigma1(w15) + w10 + sigma0(w2)));
Round(g, h, a, b, c, d, e, f, 0x0fc19dc6 + (w2 += sigma1(w0) + w11 + sigma0(w3)));
Round(f, g, h, a, b, c, d, e, 0x240ca1cc + (w3 += sigma1(w1) + w12 + sigma0(w4)));
Round(e, f, g, h, a, b, c, d, 0x2de92c6f + (w4 += sigma1(w2) + w13 + sigma0(w5)));
Round(d, e, f, g, h, a, b, c, 0x4a7484aa + (w5 += sigma1(w3) + w14 + sigma0(w6)));
Round(c, d, e, f, g, h, a, b, 0x5cb0a9dc + (w6 += sigma1(w4) + w15 + sigma0(w7)));
Round(b, c, d, e, f, g, h, a, 0x76f988da + (w7 += sigma1(w5) + w0 + sigma0(w8)));
Round(a, b, c, d, e, f, g, h, 0x983e5152 + (w8 += sigma1(w6) + w1 + sigma0(w9)));
Round(h, a, b, c, d, e, f, g, 0xa831c66d + (w9 += sigma1(w7) + w2 + sigma0(w10)));
Round(g, h, a, b, c, d, e, f, 0xb00327c8 + (w10 += sigma1(w8) + w3 + sigma0(w11)));
Round(f, g, h, a, b, c, d, e, 0xbf597fc7 + (w11 += sigma1(w9) + w4 + sigma0(w12)));
Round(e, f, g, h, a, b, c, d, 0xc6e00bf3 + (w12 += sigma1(w10) + w5 + sigma0(w13)));
Round(d, e, f, g, h, a, b, c, 0xd5a79147 + (w13 += sigma1(w11) + w6 + sigma0(w14)));
Round(c, d, e, f, g, h, a, b, 0x06ca6351 + (w14 += sigma1(w12) + w7 + sigma0(w15)));
Round(b, c, d, e, f, g, h, a, 0x14292967 + (w15 += sigma1(w13) + w8 + sigma0(w0)));
Round(a, b, c, d, e, f, g, h, 0x27b70a85 + (w0 += sigma1(w14) + w9 + sigma0(w1)));
Round(h, a, b, c, d, e, f, g, 0x2e1b2138 + (w1 += sigma1(w15) + w10 + sigma0(w2)));
Round(g, h, a, b, c, d, e, f, 0x4d2c6dfc + (w2 += sigma1(w0) + w11 + sigma0(w3)));
Round(f, g, h, a, b, c, d, e, 0x53380d13 + (w3 += sigma1(w1) + w12 + sigma0(w4)));
Round(e, f, g, h, a, b, c, d, 0x650a7354 + (w4 += sigma1(w2) + w13 + sigma0(w5)));
Round(d, e, f, g, h, a, b, c, 0x766a0abb + (w5 += sigma1(w3) + w14 + sigma0(w6)));
Round(c, d, e, f, g, h, a, b, 0x81c2c92e + (w6 += sigma1(w4) + w15 + sigma0(w7)));
Round(b, c, d, e, f, g, h, a, 0x92722c85 + (w7 += sigma1(w5) + w0 + sigma0(w8)));
Round(a, b, c, d, e, f, g, h, 0xa2bfe8a1 + (w8 += sigma1(w6) + w1 + sigma0(w9)));
Round(h, a, b, c, d, e, f, g, 0xa81a664b + (w9 += sigma1(w7) + w2 + sigma0(w10)));
Round(g, h, a, b, c, d, e, f, 0xc24b8b70 + (w10 += sigma1(w8) + w3 + sigma0(w11)));
Round(f, g, h, a, b, c, d, e, 0xc76c51a3 + (w11 += sigma1(w9) + w4 + sigma0(w12)));
Round(e, f, g, h, a, b, c, d, 0xd192e819 + (w12 += sigma1(w10) + w5 + sigma0(w13)));
Round(d, e, f, g, h, a, b, c, 0xd6990624 + (w13 += sigma1(w11) + w6 + sigma0(w14)));
Round(c, d, e, f, g, h, a, b, 0xf40e3585 + (w14 += sigma1(w12) + w7 + sigma0(w15)));
Round(b, c, d, e, f, g, h, a, 0x106aa070 + (w15 += sigma1(w13) + w8 + sigma0(w0)));
Round(a, b, c, d, e, f, g, h, 0x19a4c116 + (w0 += sigma1(w14) + w9 + sigma0(w1)));
Round(h, a, b, c, d, e, f, g, 0x1e376c08 + (w1 += sigma1(w15) + w10 + sigma0(w2)));
Round(g, h, a, b, c, d, e, f, 0x2748774c + (w2 += sigma1(w0) + w11 + sigma0(w3)));
Round(f, g, h, a, b, c, d, e, 0x34b0bcb5 + (w3 += sigma1(w1) + w12 + sigma0(w4)));
Round(e, f, g, h, a, b, c, d, 0x391c0cb3 + (w4 += sigma1(w2) + w13 + sigma0(w5)));
Round(d, e, f, g, h, a, b, c, 0x4ed8aa4a + (w5 += sigma1(w3) + w14 + sigma0(w6)));
Round(c, d, e, f, g, h, a, b, 0x5b9cca4f + (w6 += sigma1(w4) + w15 + sigma0(w7)));
Round(b, c, d, e, f, g, h, a, 0x682e6ff3 + (w7 += sigma1(w5) + w0 + sigma0(w8)));
Round(a, b, c, d, e, f, g, h, 0x748f82ee + (w8 += sigma1(w6) + w1 + sigma0(w9)));
Round(h, a, b, c, d, e, f, g, 0x78a5636f + (w9 += sigma1(w7) + w2 + sigma0(w10)));
Round(g, h, a, b, c, d, e, f, 0x84c87814 + (w10 += sigma1(w8) + w3 + sigma0(w11)));
Round(f, g, h, a, b, c, d, e, 0x8cc70208 + (w11 += sigma1(w9) + w4 + sigma0(w12)));
Round(e, f, g, h, a, b, c, d, 0x90befffa + (w12 += sigma1(w10) + w5 + sigma0(w13)));
Round(d, e, f, g, h, a, b, c, 0xa4506ceb + (w13 += sigma1(w11) + w6 + sigma0(w14)));
Round(c, d, e, f, g, h, a, b, 0xbef9a3f7 + (w14 + sigma1(w12) + w7 + sigma0(w15)));
Round(b, c, d, e, f, g, h, a, 0xc67178f2 + (w15 + sigma1(w13) + w8 + sigma0(w0)));
s[0] += a;
s[1] += b;
s[2] += c;
s[3] += d;
s[4] += e;
s[5] += f;
s[6] += g;
s[7] += h;
chunk += 64;
}
}
直接将循环展开,虽然提高了性能但却加大了存储开销(然而PC机不在乎)。(果然人类的本质是复读机)
SHA-256实现优化
由于我需要在stm32f767zit这块芯片上运行SHA-256,单片机不仅需要更高的效率,还需要较小的开销,包括RAM和Flash两方面的开销(而且不想上汇编不仅不好维护而且万一后面就不用了岂不是白费好大功夫)。所以上面两种代码均不能直接使用。(实际上上面两个程序也并不是直接使用C语言编写的代码,而是都有各自的用汇编编写的针对性优化程序,甚至使用了SIMD)这让我深刻的理解了跨平台的两种方法,一种是使用高级语言,另一种是将所有常用平台的汇编都写一遍(简称大力出奇迹)。
仔细观察上边的混合算法框图,不难发现,其实每轮便换更新的值只有两块,第一块是H的值,新的值是原来值加上所有的部分组成的,第二块是D的值,其新的值仅仅只是加上H块运算中的一个中间值。所以我们完全可以节省中间变量,先算一部分H的值,然后将H加在D上,再继续运算到结束。
对于Wt前16块与17至64块不相同需要迭代的问题,完全不需要开辟一个64块的内存或者单独来进行计算,通过观察发现,每一轮变换完全用不到16块之前的Wt值,也就是说超过当前变换轮数16块的值便可以丢弃,即当前计算结束后的Wt值在未来的第16次变换便不再需要了。所以可以在当前变换完了之后直接对之后的第16次变换所需要的值进行计算,并填在当前值的位置上,因为当前值已经不再需要了。这样不仅节省了Flash的开销,同时也节省了内存的开销,同时也不牺牲性能,可谓一举两得。
以下便是根据这几点构建的代码,可以看到整个函数只有133字节的内存开销(64字节存储Wt,32字节存储初始Hash值,32字节存储变换Hash值,4字节作为轮换临时值,1字节作为循环控制变量),并且短小精悍(疯狂自吹):
CRYPTO_STATUS sha_256_update(uint32_t* data)
{
uint8_t i;
uint32_t tmp;
memcpy(SHA256_Data2, SHA256_Data1, 32);
for (i = 0; i < 64; ++i)
{
SHA256_Data2[7] += sha256_ch(SHA256_Data2[4], SHA256_Data2[5], SHA256_Data2[6])
+ sigma_h1(SHA256_Data2[4]) + SHA256_CalcTab[i] + data[i & 0x0F];
SHA256_Data2[3] += SHA256_Data2[7];
SHA256_Data2[7] += sha256_maj(SHA256_Data2[0], SHA256_Data2[1], SHA256_Data2[2])
+ sigma_h0(SHA256_Data2[0]);
tmp = SHA256_Data2[7];
SHA256_Data2[7] = SHA256_Data2[6];
SHA256_Data2[6] = SHA256_Data2[5];
SHA256_Data2[5] = SHA256_Data2[4];
SHA256_Data2[4] = SHA256_Data2[3];
SHA256_Data2[3] = SHA256_Data2[2];
SHA256_Data2[2] = SHA256_Data2[1];
SHA256_Data2[1] = SHA256_Data2[0];
SHA256_Data2[0] = tmp;
data[i & 0x0F] += sigma_l1(data[(i + 14) & 0x0F]) + data[(i + 9) & 0x0F] + sigma_l0(data[(i + 1) & 0x0F]);
}
for (i = 0; i < 8; ++i)
{
SHA256_Data1[i] += SHA256_Data2[i];
}
return CRYPTO_SUCCESS;
}
对代码进行性能测试结果为:
===================
平台:Intel Xeon E5-2699 v4 @ 2.2GHz
编译器:MS VC++ v14.0 (优化等级:O2)
测试结果:129.6MByte/s
===================
平台:STM32F767ZIT @ 216MHz (开启指令和数据缓存,指令预取和Flash预取)
编译器:Armcc v5.06 (优化等级:O3)
测试结果:3.21MByte/s
===================
总的来说,速度还是能达到使用要求的。
PS:整个工程和源文件在后续整理注释后会上传到这里。(先偷个懒)
源文件:
(完)
